绪论+一些线性结构

绪论

了解数据结构研究的主要内容
- 研究非数值计算的程序设计问题中计算机的操作对象以及它们之间的关系和操作

掌握数据结构中涉及的基本概念

数据、数据元素、数据项、数据结构
数据结构
- 逻辑结构
  - 线性结构：线性表、栈、队列、串
  - 非线性结构：树、图
- 存储结构
  - 顺序存储
  - 链式存储
抽象数据类型

名词	解释
数据data	所有能输入到计算机中去的描述客观事物的符号。
数据元素data element	数据的基本单位，也称结点（node）或记录（record）
数据项data item	有独立含义的数据最小单位，也称域(field)
数据对象data object	相同特性数据元素的集合，是数据的一个子集。
数据结构data structure	是相互之间存在一种或多种特定关系的数据元素的集合。逻辑结构&存储结构&运算
抽象数据类型	ADT=(D, S, P)：数据对象&D上的关系集&D上的操作集

掌握算法的时间、空间复杂度及其分析的简易方法
- 算法5个特性：有穷性、确定性、可行性、输入、输出。
- 评价算法优劣：正确性、可读性、健壮性、高效性。
- 时间复杂度T(n)
  - 找出语句频度最大的那条语句作为基本语句
  - 计算基本语句的频度得到问题规模n的某个函数f(n)
    - 排序：n=记录数；
    - 矩阵：n=矩阵的阶数
    - 多项式：n=项数
    - 集合：n=元素个数
    - 树：n=结点个数
    - 图：n=顶点数或边数
  - 取其数量级用符号“O”表示，取最高量级并去掉系数。
  - $$
    O(1)<O(log_2n)<O(n)<O(nlog_2n)<O(n^2)<O(2^n)
    $$
    
    常数阶、对数阶、线性阶、线性对数阶、平方阶、立方阶、指数阶。

线性表

了解线性结构的特点
- 只有一个首结点和尾结点；
- 所有结点都最多只有一个直接前趋和一个直接后继。
熟练掌握顺序表的定义、查找、插入和删除
- $$
  (a_1,a_2,…,a_n)
  $$
  
  数据元素的有限序列，n=表长，n=0时是空表。
- 插入在第i个元素前：移动n-i+1次
- 删除第i个结点：移动n-i次
熟练掌握链表的定义、创建、查找、插入和删除
- 头结点、头指针、首元结点
  - 头指针是指向链表中第一个结点的指针
  - 首元结点是指链表中存储第一个数据元素的结点
  - 头结点是在链表的首元结点之前附设的一个结点；数据域内只放空表标志和表长等信息，此结点不能计入链表长度值。
    - 便于首元结点的处理
    - 便于空表和非空表的统一处理
- 单链表、循环链表、双向链表
  - 单链表：由表头唯一确定，因此可以用头指针的名字来命名。
- 循环链表
  - 循环条件：p->next!=NULL&&p->next!=L
    - 一般给出尾指针rear
  - 双向链表
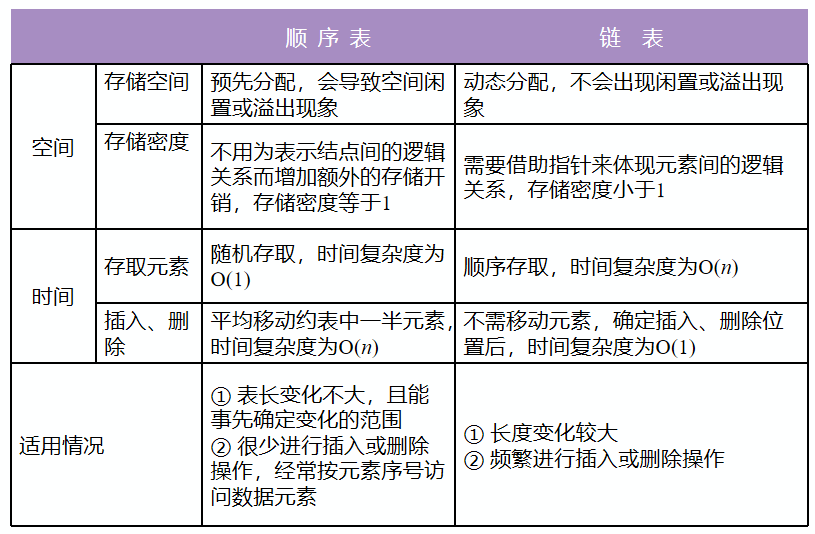
- 顺序存取：逻辑上相邻的数据元素在物理上不一定相邻
能够从时间和空间复杂度的角度比较两种存储结构的不同特点及其适用场合

栈&队列

掌握栈和队列的特点，并能在相应的应用问题中正确选用
- 后入先出：LIFO
- 先入先出：FIFO
熟练掌握栈的顺序栈和链栈的基本操作实现算法，特别应注意栈满和栈空的条件
- 链栈没有附加头结点，栈顶指针就是链表头指针；
- 栈满：top-base=stacksize;
- 栈空：top=base
- 入栈
  1
  2
  1.S.top++=e;
  2.p->next=S;S=p;
- 出栈
  1
  2
  1.e=*--S.top;
  2.p=S;S=S->next;delete p;
熟练掌握循环队列和链队列的基本操作实现算法，特别注意队满和队空的条件
- 队满
  - 循环队列中另外设一个标志以区别：(rear+1)%M==front
- 队空：front==rear
- 长度：(rear-front+M)%M
- 入队
  1
  2
  3
  1.base[rear++]=x;
  2.base[rear]=x;rear=(rear+1)%M;
  3.Q.rear->next=p;Q.rear=p;
- 出队
  1
  2
  3
  1.x=base[front++];
  2.x=base[front];front=(front+1)%M;
  3.p=Q.front->next;Q.front->next=p->next;delete p;
- 链队列：front不存储元素，是头结点，rear指向队尾，有元素
- 顺序队列（包括循环队列）中的rear设为空，而front处有元素。
理解递归算法执行过程中栈的状态变化过程
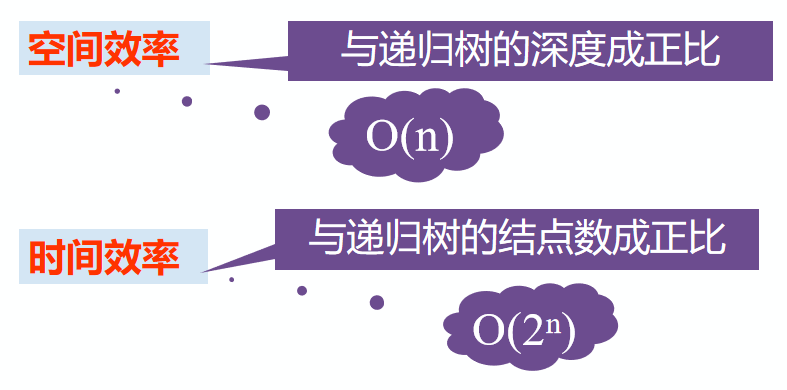
- 优点：结构清晰，程序易读。缺点：每次调用要生成工作记录，保存状态信息，入栈；返回时要出栈，恢复状态信息。时间开销大。
- 效率
掌握表达式求值方法

栈与递归

递归→非递归：

尾递归、单项递归→循环结构
自用栈模拟系统的运行时栈

串&数组&广义表

了解串的存储方法，理解串的两种模式匹配算法，重点掌握BF算法。
明确数组和广义表这两种数据结构的特点，掌握数组地址计算方法，了解几种特殊矩阵的压缩存储方法。
掌握广义表的定义、性质及其GetHead和GetTail的操作。

串相关函数

串拷贝：strcpy()
求子串的位置：Index()
串替换：Replace()
子串插入：StrInsert()
子串删除：StrDelete()
串销毁：DestroyString()

串存储

第一个位置存储长度等信息，串值的序号从1开始

顺序存储
链式存储
- 可自定义块的大小
- 存储密度低
存储密度=串值所占存储位/实际分配

next函数求值

next[j]=最长公共前后缀+1；

条件：最长公共前后缀长度小于当前子串指针前的字符个数。

next[1]=0, next[2]=1

数组

可以是链式的。

定位

a=Loc(0,0,…,0)，m表示该维的元素数量
$$
LOC(i_1,i_2,…,i_n)=a+(\sum_{j=1}^{n-1}{i_j\prod_{k=j+1}^{n}{m_k}})+i_n
$$
二维：以行序为主序和以列序为主序*

特殊矩阵

压缩存储：若多个数据元素的值都相同，则只分配一个元素值的存储空间，且零元素不占存储空间。

对称矩阵：只存储上三角或下三角，n(n+1)/2
对角矩阵：非零元素集中在主对角线及其两侧共L(奇数)条对角线的带状区域内 — L对角矩阵。以对角线的顺序存储，(n-2)L+(L+1)
三角矩阵：重复元素共享一个空间，n(n+1)/2+1
稀疏矩阵
- 顺序存储
  - 三元组表
  - 行逻辑联结
- 链式存储：十字链表

广义表

$$
LS=(a_0,a_1,…,a_{n-1})
$$

n=0为空表

长度：元素个数，元素可以是子表
深度：括号的层数
GetHead()
GetTail()
线性表是一种特殊的广义表

链式存储

表结点
原子结点

Sean's Blog

线性结构部分

绪论

线性表