查找排序
查找
- 熟练掌握顺序表和有序表(折半查找)的查找算法及其性能分析方法;
- 熟练掌握二叉排序树的构造和查找算法及其性能分析方法;
- 掌握二叉排序树的插入算法,掌握二叉排序树的删除方法;
- 熟练掌握哈希函数(除留余数法)的构造;
- 熟练掌握哈希函数解决冲突的方法及其特点
查找中的概念
- 查找表:由同一类型的数据元素(或记录)构成的集合
- 静态查找表:查找的同时对查找表不做修改操作(如插入和删除)
- 动态查找表:查找的同时对查找表具有修改操作
- 关键字:记录中某个数据项的值,可用来识别一个记录
- 主关键字:唯一标识数据元素
- 次关键字:可以标识若干个数据元素
平均搜索长度
ASL:关键字的平均比较次数
$$
ASL=\sum_{i=1}^{n}{p_i*c_i}
$$
pi:查找第i个记录的概率 ( 通常认为pi =1/n );
ci:找到第i个记录所需的比较次数。
线性表的查找
顺序查找
适用于静态查找表
改进:将哨兵(即待查找的key)存入表头,从后往前
空间复杂度:一个辅助空间
时间复杂度:
- 成功:$ASLs=\frac{1}{n}*(1+2+…+n)=\frac{n+1}{2}$
- 失败:$ASLf=\frac{1}{n}n(n+1)=(n+1)$
查找概率相等时,ASL相同。
查找概率不等时,如果从前向后查找,则按查找概率由大到小排列的有序表其ASL要比无序表ASL小。
折半查找
适用顺序存储结构的有序表
- 设表长为n,low、high和mid分别指向待查元素所在区间的上界、下界和中点,k为给定值
- 初始时,令low=1,high=n,mid=(low+high)/2
- 让k与mid指向的记录比较
- 若k==R[mid].key,查找成功
- 若k<R[mid].key,则high=mid-1
- 若k>R[mid].key,则low=mid+1
- 重复上述操作,直至low>high时,查找失败
时间复杂度:
$$
O(log_2n)
$$
判定树
根结点就是第一次进行比较的中间位置的记录;
前子表的中间位置作为左子树的结点;
后子表的中间位置作为右子树的结点;
查找成功时比较次数不超过判定树的深度d:
$$
d=\lfloor{log_2n}\rfloor-1
$$
查找失败时比较d或d-1次
分块查找
分块有序,即分成若干子表,要求每个子表中的数值都比后一块中数值小,然后将各子表中的最大关键字构成一个索引表,表中还要包含每个子表的起始地址。
适用线性表既要快速查找又经常动态变化。
- 索引表有序→折半查找
- 确定了待查关键字所在的子表后,在子表内采用顺序查找法
$$
ASL=L_b+L_w
$$
$$
ASL_{bs}≈log_2(\frac{n}{s}+1)+\frac{s}{2}, (log_2n\leq ASL_bs\leq \frac{n+1}{2})
$$
树表
表结构在查找过程中动态生成。对于给定值key若表中存在,则成功返回;否则插入关键字等于key 的记录
二叉排序树
性质
- 若其左子树非空,则左子树上所有结点的值均小于根结点的值;
- 若其右子树非空,则右子树上所有结点的值均大于等于根结点的值;
- 其左右子树本身又各是一棵二叉排序树
中序遍历二叉排序树能得到一个递增序列。
查找
- 若二叉排序树为空,则查找失败,返回空指针。
- 若二叉排序树非空,将给定值key与根结点的关键字T->data.key进行比较
- 若key等于T->data.key,则查找成功,返回根结点地址;
- 若key小于T->data.key,则进一步查找左子树;
- 若key大于T->data.key,则进一步查找右子树。
$$
log_2n\leq ASL\leq \frac{n+1}{2}
$$
插入
- 树中已有,不再插入
- 树中没有,查找直至某个叶子结点的左子树或右子树为空为止,则插入结点应为该叶子结点的左孩子或右孩子:插入的元素一定在叶结点上
生成
插入→生成
树的形态与插入次序有关
删除
- 删除叶节点:将双亲结点指针清除即可;
- 被删结点缺左/右子树:用其右/左子女顶替delete结点;
- 被删结点的左右子树都存在:
- 用p的直接前驱结点代替p;
- 用p的直接后继结点代替p;
平衡二叉树AVL
平衡因子:该结点左子树与右子树的高度差
平衡二叉树:任一结点的平衡因子只能是-1、0、1,即左右高度差不超过1.
平衡旋转
插入:插入后进行调整,最后仍是平衡二叉树。
B-树
m阶B-树:
- 每一个结点分支数≤m→关键字数≤m-1;
- 根结点分支数≥2(要求此根结点不为叶子结点)
- 其余分支结点的分支数≥ m/2 (向上取整)
- 所有叶子结点在同一层;
- 有序性,看PPT71
插入
若溢出,分解结点。?
- 将中间值往上提一层,调整
- 如果向上提后又溢出,继续上提
删除
若删除的关键字不在叶子结点中,用其前驱或后继来替换,删除后进行调整?,使其仍为B-树。
哈希表
哈希方法:
哈希函数:记录的存储位置与关键字之间存在对应关系
哈希冲突:不同的关键码映射到同一个哈希地址
同义词:具有相同函数值的两个关键字
哈希函数的构造
- 直接定址法;
- 关于关键码的线性函数:Hash(key) = a·key + b
- 数字分析法;
- 取关键字的若干位或组合作为哈希地址
- 平方取中法
- 将关键字平方后取中间几位作为哈希地址
- 折叠法
- 将关键字分割成位数相同的几部分(最后一部分可以不同),然后取这几部分的叠加和作为哈希地址
数位叠加 - 移位叠加:低位对齐相加
- 间界叠加:从一端到另一端沿分割界来回折迭,然后对齐相加。
- 将关键字分割成位数相同的几部分(最后一部分可以不同),然后取这几部分的叠加和作为哈希地址
- 除留余数法
- Hash(key)=key mod p,p≤表长且为质数
- 随机数法
评价因素
- 构造简单
- 均匀映射
冲突处理
开放定址法
有冲突时就去寻找下一个空的哈希地址
线性探测法
- (Hash(key)+1)mod p
- “聚集”现象
二次探测法
- $$
(Hash(key)\pm{1^2})
$$
- $$
伪随机探测法
- (Hash(key)+random)mod m,m表示表长
链地址法
相同哈希地址的记录链成一单链表,m个哈希地址就设m个单链表,然后用用一个数组将m个单链表的表头指针存储起来,形成一个动态的结构
查找效率
ASL取决于:
- 哈希函数
- 处理冲突的方法
- 哈希表的装填因子α=表中填入记录数/哈希表的长度
- α越大,发生冲突的可能性就越大,查找时比较次数就越多
$$
ASL≈1+\frac{α}{2} (拉链法)
$$
$$
ASL≈\frac{1}{2}(1+\frac{1}{1-α})(线性探测法)
$$
$$
ASL≈-\frac{1}{α}ln(1-α)(随机探测法)
$$
排序
掌握排序的基本概念和各种排序方法的特点,并能加以灵活应用
熟练掌握直接插入排序、折半插入排序、起泡排序、直接选择排序、快速排序的排序算法及其性能分析
掌握希尔排序、归并排序、堆排序、基数排序的方法及其性能分析
掌握外部排序方法中败者树的建立及归并方法,掌握置换-选择排序的过程和最佳归并树的构造方法。
内部排序&外部排序
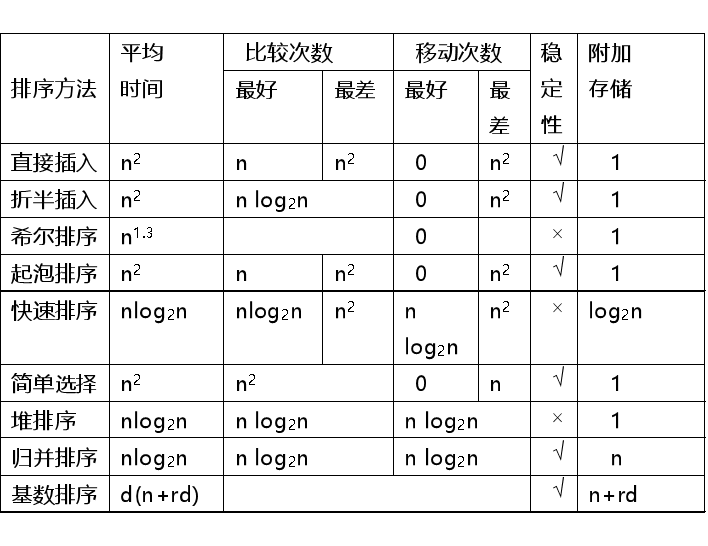
算法评价=时间效率+空间效率+稳定性
插入排序
每步将一个待排序的对象,按其关键码大小,插入到前面已经排好序的一组对象的适当位置上,直到对象全部插入为止。
直接插入排序
基于顺序查找,=n-1次插入
- 在R[1..i-1]中查找R[i]的插入位置,R[i].key< R[j+1..i-1].key;
- 将R[j+1..i-1]中的所有记录均后移一个位置;
- 将R[i] 插入到R[j+1]的位置上。
折半插入排序
基于折半查找,在插入第 i 个对象时,需要经过log2i+1(向下取整) 次关键码比较,才能确定它应插入的位置 。
希尔排序
基于逐次缩小增量
先将整个待排记录序列分割成若干子序列,分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行一次直接插入排序。
子序列的构成:相隔d增量的记录组成→逐渐缩短增量直至d=1。
最后一个增量值必须为1
不宜在链式存储结构上实现。
交换排序
两两比较,如果发生逆序则交换,直到所有记录都排好序为止
起泡排序
每趟不断将记录两两比较,并按“前小后大” 规则交换
快速排序
- 任取一个元素 (如第一个) 为中心
- 所有比它小的元素一律前放,比它大的元素一律后放,形成左右两个子表;
- 对各子表重新选择中心元素并依此规则调整,直到每个子表的元素只剩一个
从两头向中间交替式逼近
递归
选择排序
每一趟在后面 n-i +1个中选出关键码最小的对象, 作为有序序列的第 i 个记录
简单选择排序
树形选择排序
优势:利用上次选择的结果,选出次最小者。
堆排序
将序列看成完全二叉树,非终端结点的值均小于或大于左右子结点的值。(实际上是线性空间)
堆顶元素为max(大根堆)或min(小根堆)
建堆
有n 个结点的完全二叉树,最后一个分支(非终端)结点的标号是 n/2(向下取整)
设x=n/2(向下取整),从第x个元素起,至第一个元素止,进行反复筛选。
筛选法
(以小根堆为例):
- 将序列画成完全二叉树;
- 从最后一个分支点(n/2)向下取整 开始调整;
- 比较该结点与其左右子结点的大小,找出最小的那个置于该结点(交换位置),并观察位置变化后的左右子树是否符合小根堆的要求,递归调整。
调整
在输出堆顶元素后重新调整为新堆。
- 输出堆顶元素后,以堆中最后一个元素替代之
- 将根结点与左、右子树根结点比较,并与小者交换
- 重复直至叶子结点,得到新的堆
归并排序
将两个或两个以上的有序表组合成一个新有序表
2-路归并排序
- 初始序列看成n个有序子序列,每个子序列长度为1
- 两两合并,得到 n/2 (向下取整)个长度为2或1的有序子序列
- 再两两合并,重复直至得到一个长度为n的有序序列为止
类比多项式相加
基数排序
最高位优先MSD
- 先对最高位关键字k1(如花色)排序,将序列分成若干子序列,每个子序列有相同的k1值;
- 然后让每个子序列对次关键字k2(如面值)排序,又分成若干更小的子序列;
- 依次重复,直至就每个子序列对最低位关键字kd排序,就可以得到一个有序的序列。
eg.十进制数比较
最低位优先LSD
- 首先依据最低位排序码Kd对所有对象进行一趟排序。
- 再依据次低位排序码Kd-1对上一趟排序结果排序。
- 依次重复,直到依据排序码K1最后一趟排序完成,就可以得到一个有序的序列。
链式基数排序
条件:
- 知道各级关键字的主次关系
- 知道各级关键字的取值范围
步骤:
- 首先对低位关键字排序,各个记录按照此位关键字的值‘分配’到相应的序列里。
- 按照序列对应的值的大小,从各个序列中将记录‘收集’,收集后的序列按照此位关键字有序。
- 在此基础上,对前一位关键字进行排序
外部排序
- 按可用内存大小,利用内部排序方法,构造若干个记录的有序子序列写入外存,通常称这些记录的有序子序列为 “归并段”;
- 通过“归并”,逐步扩大(记录的)有序子序列的长度,直至外存中整个记录序列按关键字有序为止。