Sean's Blog
0%

树和图

发表于 更新于 分类于 ，

树和图的介绍

树&二叉树

  • 掌握二叉树的基本概念、性质和存储结构
    • 有序性
  • 熟练掌握二叉树的前、中、后序遍历方法
  • 了解线索化二叉树的思想
  • 熟练掌握：哈夫曼树的实现方法、构造哈夫曼编码的方法
  • 了解：森林与二叉树的转换，树的遍历方法

树的表示形式：倒悬树、嵌套集合、广义表形式、凹入法。

二叉树的性质

  • 第i层上有$2^{i-1}$个结点

  • 至多有$2^k-1$个结点

  • $n_0=n_2+1$

  • 完全二叉树的深度：
    $$
    \lfloor log_2n \rfloor +1
    $$

  • 完全二叉树的编号

    • 双亲：$\lfloor i/2 \rfloor$
    • 左孩子：$2i$
    • 右孩子：$2i+1$

二叉树的存储

  • 顺序存储：按结点编号存放，适于存满二叉树和完全二叉树。
  • 链式存储
    • 二叉链表：存放左右孩子的指针，有n+1个空指针域
    • 三叉链表：+双亲结点

二叉树的遍历

x序遍历表示根结点的位置，如先序遍历的顺序是根左右，中序是左根右，后序是左右根。

  • 先序—包围圈
  • 中序—压成一条线
  • 后序—摘葡萄

根据遍历顺序构造二叉树

(26条消息) 根据中序遍历和后序遍历构造二叉树_Nan_Feng726的博客-CSDN博客_根据后序遍历和中序遍历构造二叉树

  • 后序+中序
    1. 后续遍历的最后一个元素是根结点
    2. 根据根节点在中序遍历中进行切分，左边为左子树，右边为右子树
    3. 找出左子树的根结点，继续切分，重复操作。
  • 先序+中序
    1. 先序遍历的第一个元素是根结点
    2. 同上

线索化二叉树

lchild LTag data RTag rchild
  • 若结点有左子树，LTag=0，lchild指向其左孩子；否则，LTag=1， lchild指向其直接前驱(即线索)；
  • 先序/中序/后序线索化二叉树
  • 二叉链表空间效率低是出现线索化二叉树出现的原因

树的存储

森林转为二叉树

森林转化为二叉树（详解版） (biancheng.net)

  1. 将森林中的普通树全部化为二叉树
    1. 孩子兄弟表示法—二叉链表
      从树的根节点开始，依次用链表存储各个节点的孩子节点和兄弟节点。
    2. 转化出来的二叉树根节点是不会有右孩子的！因为原树的根节点没有兄弟节点。
  2. 将森林中第一棵树的树根作为整个森林的树根，其他树的根节点看作是第一棵树根节点的兄弟节点，采用孩子兄弟表示法将所有树进行连接；

哈夫曼树

前缀编码：每一码都不是另一码的前缀，二叉树中左-0，右-1；

哈夫曼编码的译码过程：分解接收字符串，遇”0”向左，遇”1”向右；一旦到达叶子结点，则译出一个字符，反复由根出发，直到译码完成。

一些概念：

  • 路径
  • 路径长度
  • 带权路径长度：结点到根的路径长度与结点上权的乘积
  • 树的带权路径长度：树中所有叶子结点的带权路径长度之和
  • 哈夫曼树：带权路径长度最小的树。
  • 一棵有n个叶子结点的Huffman树有 2n-1个结点

构造

  1. 把所有元素放入等待区；
  2. 找出最小的两个，形成新的结点放入等待区，并在等待区删除这两个最小的；
  3. 再在等待区找出两个最小的，重复。

图

  • 掌握：图的基本概念及相关术语和性质
  • 熟练掌握：图的邻接矩阵和邻接表两种存储表示方法
  • 熟练掌握：图的两种遍历方法DFS和BFS
  • 熟练掌握：最短路算法（Dijkstra算法）
  • 掌握：最小生成树的两种算法及拓扑排序算法的思想

好多概念

  • 邻接、权与网、稀疏图、稠密图
  • 度
  • 路径、路径长度、回路、简单路径、简单回路
  • 连通图，强连通图：强弱概念只存在于有向图中，强连通表示两结点间双向连通。
  • 子图：结点和边都是母图的子集。
    • 连通分量，强连通分量：G的极大连通子图，G的极大强连通子图。
    • 极小连通子图
    • 生成树：$V_1=V$的极小连通子图
    • 生成森林：对非连通图，由各个连通分量的生成树的集合。

存储

  • 顺序存储

    • 邻接矩阵

  • 链式存储

    • 邻接表

    • 邻接多重表

    • 十字链表

      • 结点表

        data firstin firstout

      • 边结点表

        info tailvex headvex hlink tlink

邻接矩阵

  • 输入总顶点数和总边数。
  • 依次输入点的信息存入顶点表中。
  • 初始化邻接矩阵，使每个arcs[i][j]初始化为极大值。
  • 构造邻接矩阵
    • 输入有关联的两个顶点的下标i,j；
    • 将对应的arcs[i][j]置为1。

邻接表

对每个顶点vi 建立一个单链表，把与vi有关联的边的信息链接起来，每个结点设为3个域；

每个单链表的头结点另外用顺序存储结构存储。

头结点=数据域+链域

表结点=邻接点域+链域+数据域

  • 输入总顶点数和总边数
  • 依次输入点的信息存入顶点表中(G->vertices[i].data)，使每个表头结点的指针域初始化为NULLG->vertices[i].firstarc=NULL。
  • 创建邻接表。
    • 输入下标对；
    • 用头插法将边结点插入相应的单链表中；

在邻接矩阵和邻接表确定的情况下遍历序列结果是唯一的；

最小生成树

生成树：包含图G所有顶点的极小连通子图（n-1条边）

  • DFS生成树
  • BFS生成树

最小生成树：权值之和最小的生成树

贪心算法

以当前情况为基础作最优选择，而不考虑各种可能的整体情况，所以贪心法不要回溯,有时不一定是最优解。

Prim算法

归并顶点，适于稠密网。

  1. 从某顶点 u0 出发，选择与它关联的具有最小权值的边(u0, v)，将其顶点加入到生成树的顶点集合U中
  2. 每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(u, v),把它的顶点加入到U中
  3. 直到所有顶点都加入到生成树顶点集合U中

Kruskal算法

归并边，适于稀疏网。

  1. 构造一个只有 n个顶点，没有边的非连通图 T = { V, E }, 每个顶点自成一个连通分量
  2. 在 E 中选最小权值的边,若该边的两个顶点落在不同的连通分量上，则加入 T 中；否则舍去，重新选择
  3. 直到所有顶点在同一连通分量上为止

最短路径

最短路径与最小生成树不同，路径上不一定包含n个顶点

Dijkstra算法

单源最短路径——某指定顶点到其余各顶点

  1. 初始化：先找出从源点$v_0$到各终点$v_k$的直达路径（$v_0$,$v_k$），即通过一条弧到达的路径。

  2. 选择：最短距离对应的顶点成为当前最短路径的顶点

  3. 更新：若存在(u,$v_k$)使得（u在最短路径的顶点集合中）
    $$
    (v_0,u)+(u,v_k)<(v_o,v_k)
    $$
    则以路径($v_0$,u,$v_k$)代替($v_0$,$v_k$)。

另：

  1. 将结点分为S，T两个集合
    • S集合中最开始只有$v_0$，
    • T=V-S。
    • T中顶点对应的距离值用辅助数组D存放。D[i]初值=<$v_0,v_i$>的权值或无穷大。
  2. 从T中选取一个距离最小的顶点加入S。
  3. 对T中顶点的距离值进行更新。

Floyd算法

任意两顶点之间的最短路径

拓扑排序

  1. 选一个没有直接前驱的顶点, 并输出之；
  2. 从图中删去该顶点, 同时删去所有它发出的有向边;
  3. 重复。
  4. 若最后图中还有未输出的顶点，但已跳出处理循环。这说明剩下一些顶点都有直接前驱，，这时AOV网络中必定存在有向环

关键路径

AOE网

  • 事件：ve(vi), vl(vi), vi表示结点，事件最早或最晚发生时间，瞬时时间。

    • ve(1)=0
    • vl(n)=ve(n);

  • 活动：e(ai), l(ai), ai表示边，活动最早或最晚开始时间。

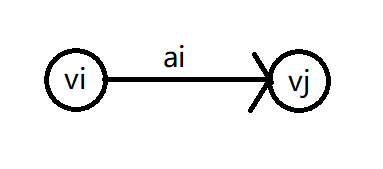
image-20211218203652634

  • $$
    e(a_i)=ve(v_i),ve(i)=Max{ve(v_{pre})+w_{pre,i}}
    $$

  • $$
    l(a_i)=vl(v_j)-w_{i,j},vl(v_j)=Min{vl(v_{next})-w_{j,next}}
    $$

  • 关键活动：l(ai)=e(ai)