参考的书《计算机组成与体系结构》第4版(黑皮书)(The Essentials of Computer Organization and Architecture)。注:目前仅记录考试需要用到的部分。
2.2按位计数系统
Positional Numbering Systems
base-2系统:以2为基数,按位存储数字表示2的幂次。
基数base:某个数能以基数的幂次方相加来表示。base==radix
2.3进制之间的转换
radix conversation/converting between bases
decimal-10,ternary-3,hexadecimal-16
无符号整数的转换
- 减法subtraction-先得到高位
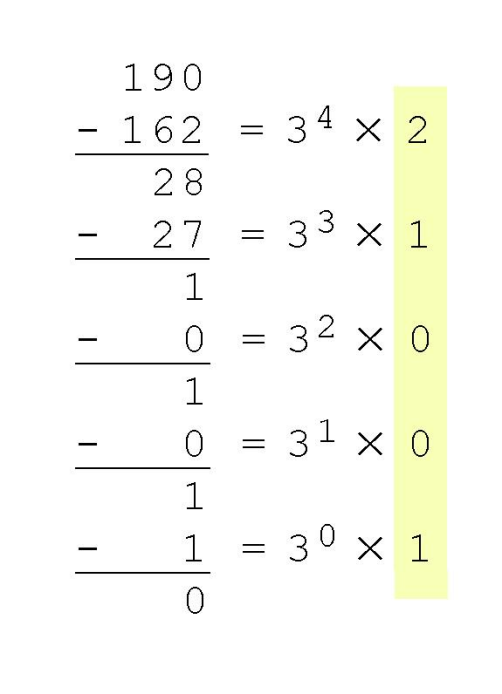
- 除法余数division remainder-先得到低位
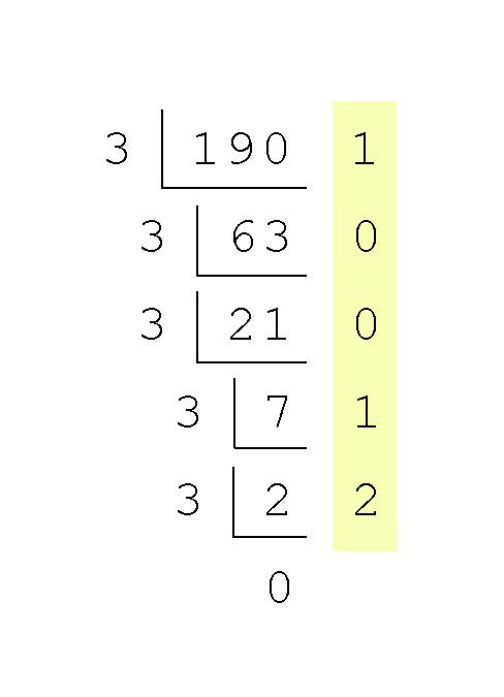
小数的转换
小数decimal不一定在所有进制下都有精确的表示。
小数点右边表示基数的负幂次negative powers of the radix
- 减法(减负次幂)-先得到高位(更靠近小数点)

- 乘法multiplication-也是先得到高位(只能是高位,如果能得到地位那一定有精确表示?)

2的幂次作为基数的计数系统之间的转化
二进制八进制十六进制之间的转换:一位8进制数可直接写为3位2进制;一位16进制数可直接写为4位2进制。如果位数不够(3/4)左侧补零
八进制适用于使用6位字的系统
2.4有符号整数表示
unsigned/signed numbers有/无符号数
signed magnitude符号幅度(我觉得是原码
原码
最高位表示符号sign:0正1负;其余位表示数值。
补码
complement system补码系统,one’s complement一位补码即反码,two’s complement补码
以r为底 的d位非零数N的基数补码是r^d – N。简单来算:正数的补码就是原码;负数的补码是原码按位取反(得到反码),然后末端加1得到补码。通过加负数的补码实现二进制减法
移码
Excess-M/offset binary移码:以无符号值表示有符号值。
通常选择的偏差bias:$M=2^{n-1}-1$。
计算excess-M:十进制+M再转为二进制(此时的的二进制)
示例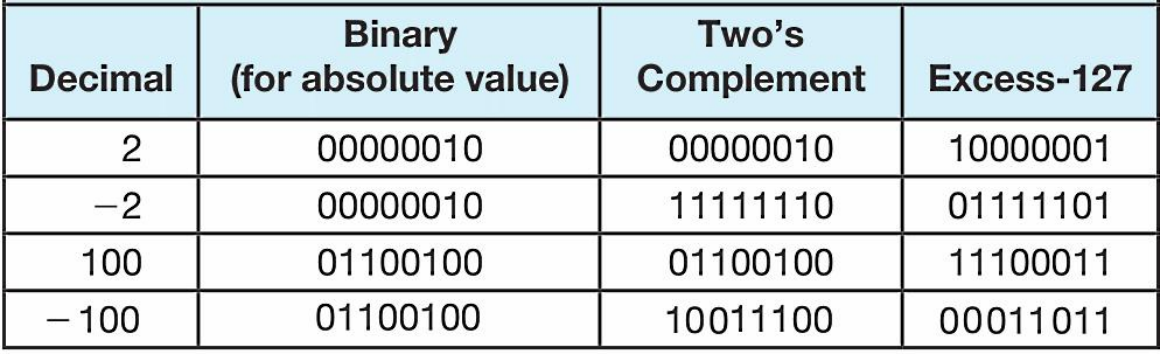
进位和溢出
overflow
检测补码系统中溢出的规则:如果符号位的’carry in’=’carry out’就没有发生溢出;不等就是溢出了。carry in就是从数值位进到符号位,carry out就是符号位上产生的进位。
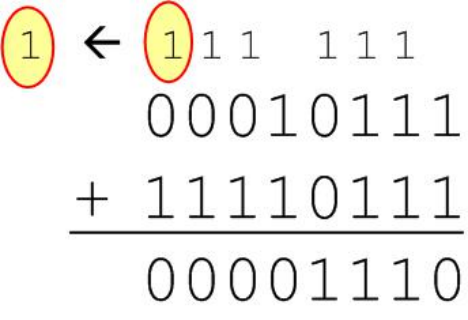
如图:carry in==carry out==1
进位与溢出是相互独立的
booth算法
- 10(乘数的当前+右侧):乘积-被乘数(上面的那个)
- 01:乘积+被乘数
- 00/11:左移一位,乘积+0
- 假设乘数位的起始位(最右侧)为0
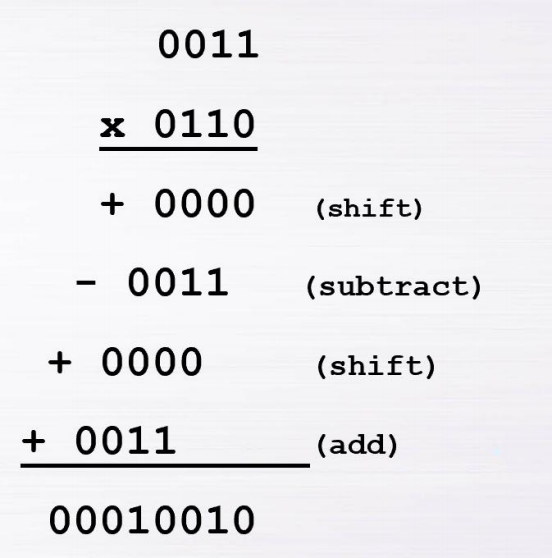
注意事项:
- 补码扩展:补高位,正数补0,负数补1

算术移位
算术移位arithmetic shift
算术左移=最右边插入0=乘2,算数右移=最左边插入0=除2.
2.5浮点数表示
floating-point浮点数,在计算机中由三个固定大小的字段组成:符号+指数(决定了可以表示的值的范围)+有效数字(一般是小数点后的,for精度)
| sign | exponent | significand |
|---|
典例-14位浮点模型simple model:len(floating-point)=14(len(exponen)=5, len(significand)=8)
eg.$32=2^5=1.02^5=0.12^6$,在14位浮点模型中表示为:(注意有效数字是小数部分,右侧补零)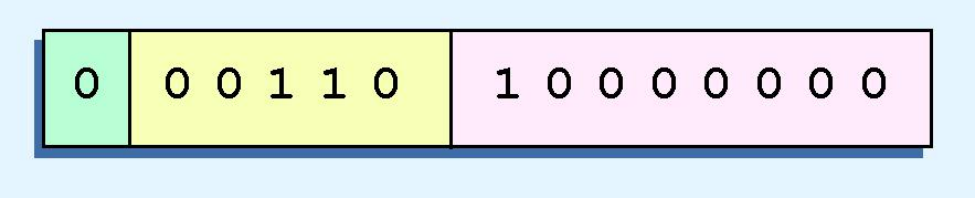
同义问题synonymous forms:由于$0.12^6=0.012^7=……$,规定有效数字的第一位必须是1(归一化);
提供负指数negative exponents:使用有偏指数biased exponent,bias=$2^{5-1}-1$=15,即excess-15
- IEEE浮点数标准规定小数点左侧必须为1.
- 避免测试浮点值是否等于0,因为0有符号位,正零不等于负零。
浮点运算
以14位浮点模型为例
加减法
将指数化为相等,使小数点对齐?然后有效数字段是正常的二进制加法,如有进位,则调整指数。
eg.$12_{10}=0.11002^4,1.25_{10}=0.0001012^4$,excess-15,可得:指数=4+15=19=10011,计算过程如下: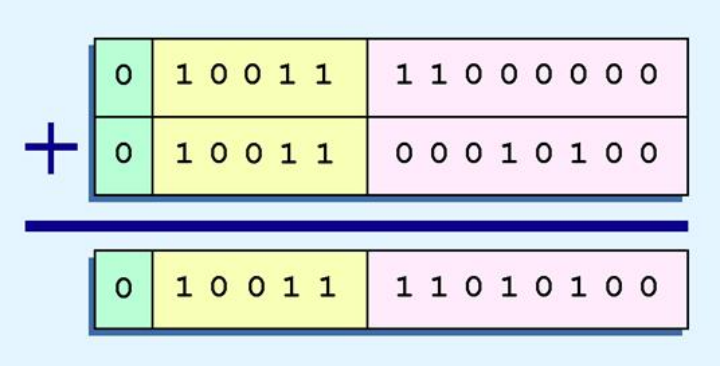
乘除
不需要将指数调至相等。有效数字跟正常的二进制乘法一样,计算结束后调整指数。
浮点误差
eg.$128.5_10=10000000.1_2=0.100000001*10^8$,若使用14位浮点模型则不能准确表示,因为有效数字只有8位,而128.5有9位,低位会丢失(变成128)。此时的相对误差为:
$$
\frac{128.5-128}{128.5}≈0.39%
$$
- 由于位会被截断,不一定满足交换律和分配率
上溢下溢
浮点上溢overflow和下溢underflow会导致程序崩溃
当没有空间存储计算产生的高位时,就会发生上溢
当值太小而无法存储时会发生下溢,可能导致除
以零
精度与准确性
精度precision,准确性accuracy,一般是正相关(不一定!)
2.7错误检测与纠错
error detection and correction
循环冗余校验
CRC:cycling redundancy checking
systematic error detection系统错误检测
CRC是模2算数域上的多项式
模2除法
modulo 2 division
除法过程中:模2减=模2加=按位异或,下例计算商和余数: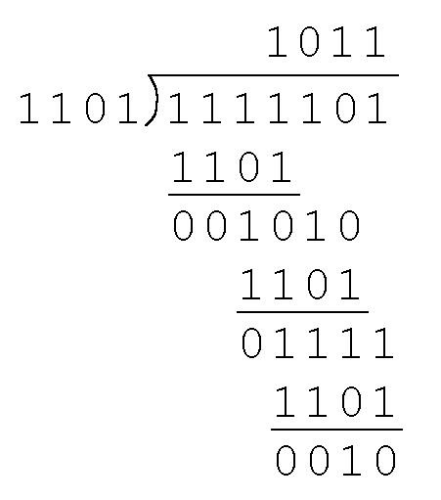
把要传输的数据的二进制格式想成域上多项式。
检测过程
- 假设传输的数据的二进制串为m1;
- 接收方和发送方商定一个k(key);
- m1左移(len(key)-1)位后得到m2;
- (模2除法)m2/key得到余数r1(remainder);
- 发送消息m3=m2+r1;
- 接收方收到m3,r2=m3/k,若r2=0则没有位丢失或损坏。
汉明码
Hamming codes
里德-所罗门码
Reed-Solomon codes
作业
1.十进制转其他进制
除法取余,先得到的是低位
5.其他进制转十进制
r进制数$a_na_{n-1}…a_1a_0$转十进制:
res=$a_n×r^n+a_{n-1}×r^{r-1}×…a_1×r+a_0$
7.十进制小数转二进制
整数与小数分开计算
小数部分乘2取整法,先得到离小数点近的
由于不一定能精确表示(不一定能最后乘得结果为1),需要注意题目要求保留几位小数
13.16进制转二进制
一位16进制数=4位二进制数,高位补零
17.原码反码补码移码
原码就是表示有符号数吧?注意题目中有要求用几位有符号数表示
0正1负!!!!
有符号数的反码,符号位不变!!!
移码Excess-M中的$M=2^{n-1}-1$
43.booth算法?
关于自己凑出来答案却看不懂这件事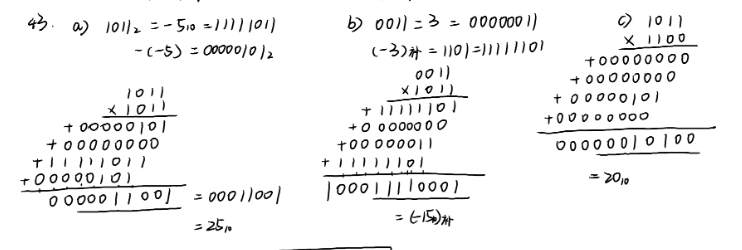
为啥要先转为八位?难道先用十进制小算一下结果?
- 10减,01加(看下面的乘数,加减上面的被乘数)
- 补码扩展时补符号位!
- 乘积结果也是补码
50.浮点数
符号位+指数位5(使用移码吗)+有效数字8
小数点对齐计算,若有效位数多了直接丢弃
78.CRC

- 被除数(message)左移len(k)-1位得到m2
- 模2除法得到余数r
- m2+r,发送
- 接收方检验:看余数是否为0