《应用密码学》
计算相关
乘法逆元
扩展欧几里得-辗转相除法:最后一个不为0的余数就是最大公约数gcd
原理:g(被除数, 除数)=g(除数, 余数)
求解x,y:xn+ay=gcd(n,a),当gcd(n,a)=1时,求乘法逆元
x乘法
面向字节,即8位,$B(x)=b_7x^7+b_6x^6+…+b_0$
AES中加法、乘法、xtime运算详述_TomPG的博客-CSDN博客_xtime
x·B(x):系数左移
- b7=1:异或
- b7=0
AES中的不可约多项式:$m(x)=x^8+x^4+x^3+x+1$
字节乘法
求:(a1 a2 a3 a4)*(b1 b2 b3 b4),均为16进制表示,即8位=字节
$$
A(x)={a1}x^3+{a2}x^2+{a3}x+{a4};\
B(x)={b1}x^3+{b2}x^2+{b3}x+{b4};\
C(x)=A(x)B(x)=\left(\begin{matrix}
a4 & a1 & a2 & a3 \
a3 & a4 & a1 & a2 \
a2 & a3 & a4 & a1 \
a1 & a2 & a3 & a4 \
\end{matrix}\right)
\left(\begin{matrix} b4\b3\b2\b1\end{matrix}\right)
$$
再根据x乘法
欧拉函数
- $\phi({p})=p-1$
- $\phi(p×q)=(p-1)*(q-1)$
- $\phi(n)=n(1-\frac1{p_1})(1-\frac1{p_2})…(1-\frac1{p_k}),(n=p_1^{a_1}p_2^{a_2}…p_k^{a_k})$
平方-乘法
快速指数乘法:https://blog.csdn.net/trigpoplar/article/details/113486172
费马小定理降幂:【指数降幂】费马小定理降幂&欧拉降幂 - Anonytt - 博客园 (cnblogs.com)
应用:
RSA
Diffie-Hellman(简化指数运算)
RSA加密+签名
求密钥
$d=e^{-1}mod n$
加密
$c=m^emodn$
平方-乘法
解密
$m=c^dmodn$
费马小定理
$a^{p-1}=1mod p$ 降幂
中国剩余定理
中国剩余定理—— 一次同余方程组解法_zorchp的博客-CSDN博客_一次同余方程的解法
ElGamal加密+签名
Elgamal加密算法和数字签名 - zeroy610 - 博客园 (cnblogs.com)
签名+验证
平方剩余的判定
椭圆曲线
密码学基础2:椭圆曲线密码学原理分析 - 简书 (jianshu.com)
Elgamal
GF(p)上的ELGamal型椭圆曲线密码详解(Java实现) - 蒙丿鑫 - 博客园 (cnblogs.com)
ECDSA
原理及安全性:[椭圆曲线数字签名算法ECDSA介绍-FreeOA](http://www.freeoa.net/osuport/sysec/ecdsa-intro_3638.html#:~:text=椭圆曲线数字签名算法 (ECDSA)是使用椭圆曲线密码 (ECC)对数字签名算法 (DSA)的模拟。 ECC 是加密算法,无法直接用于数字签名,在 ECC 之前就已经有数字签名,ECDSA就是使用 ECC 对 DSA 数字签名算法的模拟,最终签名可得到两个值 r 和 s。)
计算:椭圆曲线密码学简介(三):ECDH加密算法和ECDSA数字签名算法 - 知乎 (zhihu.com)
SHA-1
信息摘要(哈希)【密码学】一文读懂SHA-1 - 知乎 (zhihu.com)
Diffie-Hellman密钥协商
$SK:x_A,x_B。素数p,原根a$
$PK:y_A=a^{x_A}modp,y_B=a^{x_B}modp$
$协商密钥K=y_A^{x_B}modp=y_B^{x_A}modp$
Shamir门限方案
门限秘密分割方案+Lagrange插值公式
Shamir 门限方案|秘密共享|拉格朗日插值|密码学_Chels.的博客-CSDN博客_shamir门限方案
DES
加密:DES算法加密流程_lkw23333的博客-CSDN博客_des算法的加密过程
AES
(1) 字节替换:使用一个S盒对STATE的每个字节都进行独立的替换。
(2) 行移位:一个简单的移位变换。STATE的第一行保持不动,第二行循环左移动1个字节,第三行循环左移动2个字节,第四行循环左移动3个字节。
(3) 列混合:对STATE中的每列进行独立的操作,它把每个列都看成GF(2^8)中的一个多项式s(x),再与GF(2^8)上的固定多项式$a(x)={03}x^3 + {01}x^2 + {01}x + {02}$进行模x^4+1的乘法运算。
(4) 密钥加:将输入阵列和一个轮密钥进行简单的按位异或(模2加)运算。
概念
chp1 概述
对称VS非对称密码
对称密码体制中,加解密密钥相同或可相互导出;算法效率高;但密钥管理困难;开放性差;需要可靠密钥传输信道;难以实现数字签名;常用于数据加密。
非对称密码体制中每个用户有两个密钥,一个加密密钥(可公开)和一个解密密钥(保密),两个密钥不相同,且不可由公开的加密密钥导出解密密钥;密钥管理相对简单;适用于开放的应用环境;可方便实现数字签名和验证;算法计算效率较低;常用于密钥协商和数字签名。
一切秘密寓于密钥之中
对于商用密码系统而言,公开密码算法的优点包括:
1)有利于对密码算法的安全性进行公开测试评估;
2)防止密码算法设计者在算法中隐藏后门;
3)易于实现密码算法的标准化;
4)有利于使用密码算法产品的规模化生产,实现低成本和高性能。
但是必须要指出的是,密码设计的公开原则并不等于所有的密码在应用时都一定要公开密码算法。
攻击类型
- 惟密文攻击
- 已知明文攻击
- 选择明文攻击
- 选择密文攻击
选择
-
chp2 古典密码
单表替代密码
明文空间:26个英文字母的集合;
密文空间:26个英文字母的集合;
密钥空间:$K = {π: Z_{26} -> Z_{26} | π是置换}$
一般单表替代
以26个英文字母集合上的一个置换π为密钥
移位密码
0-25与a-z对应,k表示循环右移k位
加密:$c=E_k(m)=(m+k)mod26$
解密:$m=D_K(c)=(c-k)mod26$
当k=3时,为凯撒密码

仿射密码
密钥空间:$K={(k_0,k_1)| k_0,k_1∈Z_{26},gcd(k_1,26)=1}$
加密:$c=E_k(m)=(k_1*m+k_0)mod26$
解密:$m=D_K(c)=k_1^{-1}(c-k_0)mod26$ , $k_1k_1^{-1}=1mod26$ , 求逆用扩展欧几里得
k1=1时即为移位密码,而k0=0则称为乘法密码
仿射密码要求(k1, 26)=1 ,否则就会有多个明文字母对应一个密文字母的情况。由于与26互素的整数有12个,故仿射密码密钥空间大小为|K|=12×26=312。
密钥短语
将英文单词作为密钥,使字母表右移产生替换表,如下图为以key为密钥:

安全性
最大问题: 单表替代密码表现出明文中单字母出现的频率分布与密文中相同。
多表替代
使用了两个或两个以上的替代表
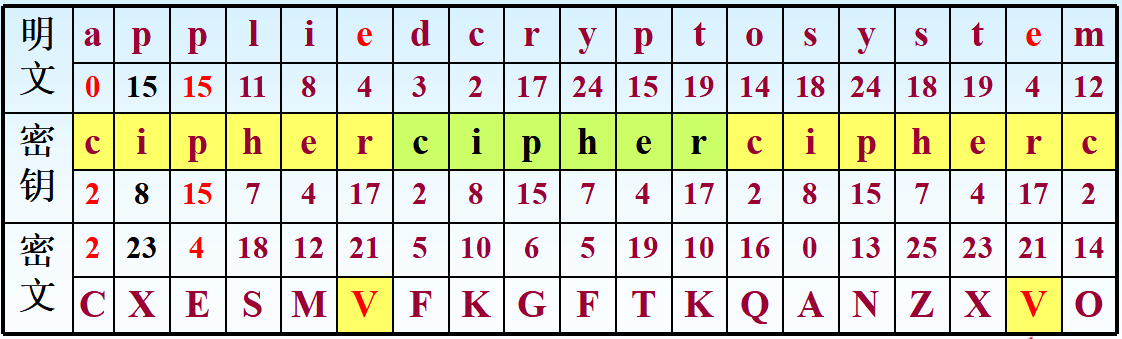
Vigenere维吉尼亚
选择一个单词作为密钥,明文按密钥大小分组,每组与密钥相加。如下图,选取cipher作为密钥,加密明文消息appliedcryptosystem:
Hill希尔
通过矩阵线性变换,密钥K是一个矩阵。
加密:C = K * M mod 26
解密:$M=K^{-1}*C\ mod26$, $K^{-1}$是K的逆矩阵
Hill密码特点:
- 可以较好地抑制自然语言的统计特性,不再有单字母替换的一一对应关系,对抗“惟密文攻击”有较高安全强度。
- 密钥空间较大,在忽略密钥矩阵K可逆限制条件下,$|K|=26^{n×n}$
- 易受已知明文攻击及选择明文攻击。
一次一密
理论上不可破译,绝对安全
playfair
Playfair密码是一种著名的双字母单表替代密码,实际上属于一种多字母替代密码。

对每一明文字母对P1、P2的加密方法如下:
(1)若P1、P2在同一行,密文C1、C2分别是紧靠P1、P2右端的字母;
(2)若P1、P2在同一列,密文C1、C2分别是紧靠P1、P2下方的字母;
(3)若P1、P2不在同一行,也不在同一列,则C1、C2是由P1、P2确定的矩形其它两角的字母,且C1和P1在同一行,C2和P2在同一行;
(4)若P1=P2,则两个字母间插入一个预先约定的字母,如x,并用前述方法处理;如balloon,则以ba lx lo on 来加密。
(5)若明文字母数为奇数,则在明文尾填充约定字母。
| 明文分组 | pl | ay | fa | ir | ci | ph | er |
|---|---|---|---|---|---|---|---|
| 密文分组 | LA | YF | PY | RS | MR | AM | CD |
周期置换密码
按周期分组

逆置换
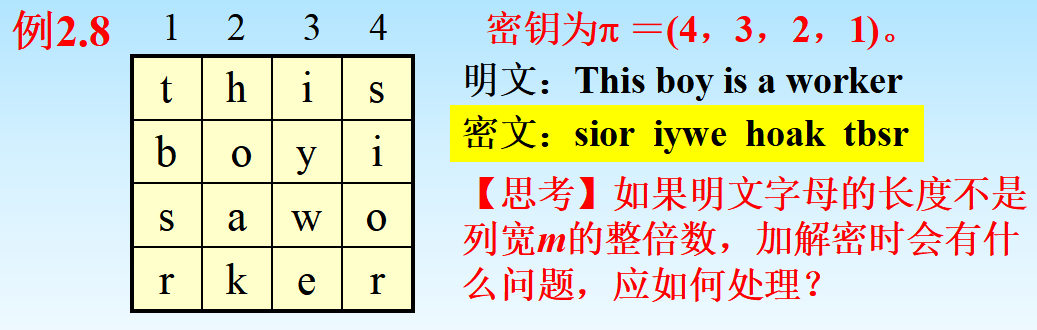
列置换
将明文按行填写到一个表格中;然后按一个置换交换列的位置次序,再按列读出即得密文。(横着放,竖着读)
Enigma轮转机
选择
- Hill密码对抗惟密文攻击的强度较高,但安全性仍不高,是线性密码,易受已知明文攻击和选择明文攻击
- Playfair双字母替代密码
- 置换密码是Hill密码的特例,也是线性变换密码
- 是基于密钥的密码